
Avant de lire cet article, nous vous conseillons de relire avec attention notre article précédent autour de la régression linéaire. Nous y avions vu que les modèles de régression linéaire se basent sur la minimisation de l’erreur résiduelle pour l’estimation de ses coefficients.
Mais, nous avions précisé que la fonction de coût pouvait engendrer une forte instabilité dans les résultats de l’estimation.
Qu’est-ce que ça veut dire concrètement ? Cela signifie que quelques légers changements dans les données peuvent produire des modèles très différents.
Par exemple, vous avez obtenu un modèle de régression linéaire à partir d’une base de données. Puis, suite à quelques correctifs sur votre base de données, vous avez finalement 2% de vos données qui changent radicalement. Vous recalculez votre modèle de régression même si vous êtes convaincu qu’il n’y aura aucune modification de votre modèle.
Et là, quelle surprise ! Votre modèle (c’est-à-dire la valeur des coefficients de chaque variable explicative) est totalement transformé.
Heureusement, il existe des techniques pour stabiliser les modèles de régression linéaire et ainsi éviter ce genre de mauvaises surprises. Nous allons voir ensemble trois techniques de régularisation : Ridge, Lasso et ElasticNet.
Rappel : Trois étapes clés pour construire le meilleur modèle de régression linéaire
- Il faut commencer par construire une fonction de coût. C’est une fonction mathématique qui mesure l’erreur que l’on commet en approximant les données. On parle aussi d’erreur induite par la modélisation.
- Ensuite, c’est l’étape de minimisation de cette fonction coût: il faut trouver les meilleurs paramètres possibles pour notre modèle afin qu’il minimise l’erreur de modélisation.
- Enfin, il faut choisir une méthode de résolution du problème. Il existe deux méthodes :
– une méthode de résolution numérique, la descente de gradient
– une méthode analytique, la méthode des moindres carrés
Principe de fonctionnement des méthodes de régularisation
Dans le cadre de la régression linéaire et pour limiter les problèmes d’instabilité des prédictions, on a recours aux techniques de régularisation. Ces méthodes vont permettre de distordre l’espace des solutions pour empêcher l’apparition de valeurs trop élevées. On parle de « rétrécissement » (en anglais, « shrinkage ») pour évoquer cette transformation spatiale de l’espace de recherche de solutions.
Pour ce faire, il s’agit de modifier un peu la fonction de coût du problème de régression linéaire en la complétant par un terme de pénalité.
Si les trois étapes clés pour construire un modèle de régression restent inchangées, il est néanmoins nécessaire d’adapter un peu la fonction de coût.
Ainsi, la fonction de coût avec pénalisation s’écrit :

Les valeurs de x et y sont données. La fonction de coût C est, par construction, une fonction des paramètres de la fonction hypothèse h.
Et, les paramètres de C définissent une droite affine.
C’est la fonction qui va gérer la pénalité selon un paramètre lambda que l’on fixe empiriquement de façon à obtenir les meilleurs résultats.
qui va gérer la pénalité selon un paramètre lambda que l’on fixe empiriquement de façon à obtenir les meilleurs résultats.
Nous vous proposons d’aller dans le détail de trois méthodes s’appuyant sur ce principe.
Première méthode de régularisation : la régression pénalisée RIDGE
La régression ridge est l’une des méthodes de pénalisation les plus intuitives. Elle s’utilise pour limiter l’instabilité des prédictions liée à des variables explicatives trop corrélées entre elles.
Cette fonction de pénalisation se base sur la norme dite L2 qui correspond à la distance euclidienne. La régression ridge revient donc à minimiser la fonction de coût suivante :
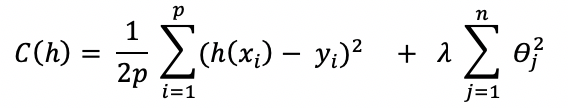
La pénalisation ridge va diminuer la distance entre les solutions possibles, sur la base de la mesure euclidienne.
Réglage du paramètre lambda :
▪ Quand lambda est proche de zéro, on s’approche de la solution classique, non pénalisée.
▪ Quand lambda est infini, la pénalisation est telle que tous les paramètres sont nuls.
▪ En augmentant lambda, on augmente le biais de la solution, mais on diminue la variance (cf. relire la définition du compromis biais-variance).
Tout comme la régression linéaire classique, la régression ridge peut être résolue par descente de gradient en itérant jusqu’à convergence pour la fonction de coût C.
La régression ridge permet donc de contourner les problèmes de colinéarité (variables explicatives très fortement corrélées entre elles) dans un contexte où le nombre de variables explicatives en entrée du problème est élevé.
La principale faiblesse de cette méthode est liée aux difficultés d’interprétation car, sans sélection, toutes les variables sont concernées dans le modèle.
Méthode de pénalisation LASSO
Si le terme LASSO appartient également au champ lexical du Far Western, LASSO ici signifie en anglais « Least Absolute Shrinkage and Selection Operator ». L’acronyme lasso contient à la fois des termes relatifs à la notion de rétrécissement (« shrinkage ») de l’espace de recherche et d’autres termes relatifs à une opération de sélection de variables (« selection operator »).
En effet, la méthode lasso introduit dans la formulation de la fonction de coût, le terme de pénalisation suivant :
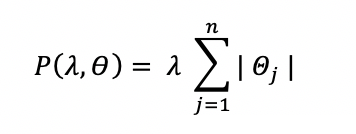
On utilise cette fois une autre norme, la norme L1 correspondant à la norme de Manhattan (distance correspondant à un déplacement à angle droit sur un damier contrairement à une distance euclidienne qui correspond à un déplacement en ligne droite).
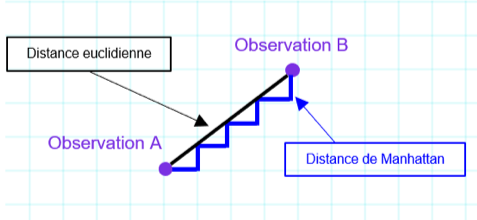 Figure 1 : Distance entre deux points : distance euclidienne versus distance de Manhattan (plusieurs chemins entre A et B)
Figure 1 : Distance entre deux points : distance euclidienne versus distance de Manhattan (plusieurs chemins entre A et B)
Il s’agit d’une distance beaucoup moins intuitive que la distance euclidienne qui va permettre une pénalisation, diminuant la distance entre les solutions possibles sur la base de la norme L1.
La fonction de coût à minimiser dans le cas du Lasso s’écrit :
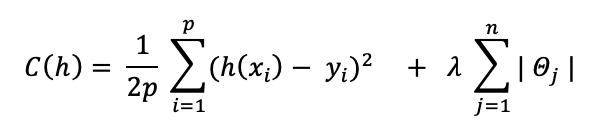
À noter qu’il n’y a pas de solution analytique pour le Lasso, on pourra donc utiliser un algorithme itératif ou bien la méthode de descente de gradient pour résoudre cette équation.
Le lasso a une propriété agréable : c’est une forme de pénalisation qui permet de rendre nul certains coefficients de variables explicatives (contrairement à la régression ridge qui pourra aboutir à des coefficients proches de 0, mais jamais strictement nuls).
Le lasso est donc un algorithme qui permet également la simplification du modèle, en éliminant des variables.
Illustrons géométriquement les effets d’une régularisation Ridge Versus Lasso sur les paramètres du modèle avec les deux graphiques ci-dessous.
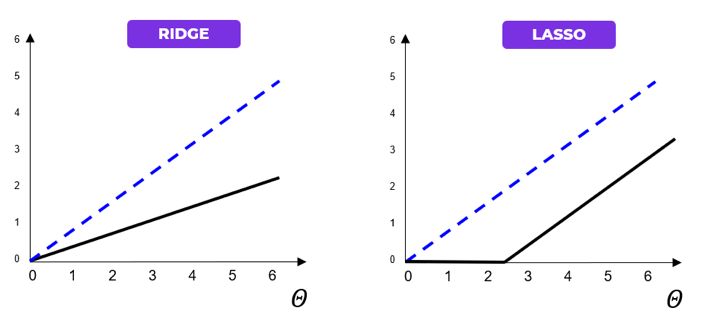
Figure 2 : Comparaison géométrique entre la régularisation RIDGE Versus LASSO sur les paramètres du modèle
Le trait noir correspond à la fonction de régularisation tandis que le trait bleu pointillé représente une droite non régularisée. On voit que la régression ridge redimensionne les coefficients en les divisant par un facteur constant alors que le lasso soustrait un facteur constant en tronquant à 0 en deçà d’une certaine valeur.
ElasticNet = RIDGE + LASSO
Dans la pratique, la régression ridge donne de meilleurs résultats que la régression pénalisée LASSO, d’autant plus si les variables explicatives du problème à résoudre sont très corrélées entre elles (c’est le cas d’usage classique de cette méthode de pénalisation).
Mais la régression ridge ne permet pas de réduire le nombre de variables. Pour trouver un compromis entre les deux techniques de pénalisation, la régularisation ElasticNet combine les deux approches.
La fonction de coût devient :
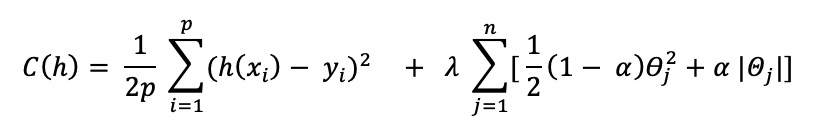
Où, le paramètre alpha est un paramètre définissant l’équilibre entre ridge et lasso.
- Pour alpha = 1, la fonction de coût correspond à celle du lasso.
- Pour alpha = 0, on retrouve la régression ridge.
Et, il est possible d’ajuster la pénalisation en fonction du cas d’application.
- Lorsque alpha s’approche de 1, on pourra avoir un comportement proche du lasso tout en éliminant les problèmes liés aux fortes corrélations entre variables explicatives.
- Lorsque alpha augmente de 0 à 1 (pour un lambda donné), le nombre de variables retirées du modèle (donc ayant un coefficient nul) augmente jusqu’à l’obtention d’un modèle le plus réduit, obtenu par lasso.
Conclusion
Pour conclure, la régularisation permet de rétrécir l’espace formé par les solutions du problème de modélisation par régression linéaire. Pour ce faire, on injecte dans la fonction de coût, un terme qui pénalisera les coefficients. Minimiser la fonction de coût minimisera ainsi les coefficients de la régression.
3 types de régularisation ont été présentés dans cet article : les méthodes ridge, lasso et elasticNet.
Dans notre prochain article, nous présenterons les approches Shapley et LIME qui permettent d’expliquer et de comprendre des modèles de machine learning complexes par des analyses graphiques simples.